


| about... | | | organizers | | | programme | | | register | | | home |
| Invited talks | ||
|---|---|---|
| David Allender | Kent | Phase separation phenomena in bilayer lipid membranes Abstract: A significant feature of many biological membranes is that the two layers, or leaflets, of their bilayer structure have different chemical compositions. Specifically the two layers contain different lipids and also have different concentrations of cholesterol. In particular, it may happen that the composition of one layer is such that it would be expected to phase separate into a fluid cholesterol-rich phase and a fluid cholesterol-poor phase, but the composition of the other layer favors miscibility. What will happen? What effect do the two layers have on each other? I will report on a study of these questions using a model based on a Landau free energy. The model includes the fact that the presence of cholesterol favors increased orientational ordering of the lipid hydrocarbon chains (i.e. reduction of the average number of gauche C-C bonds). It also includes the entropy of mixing and molecule-molecule interactions that produce phase separation, typified by a critical temperature and a critical concentration. An essential feature is that the two leaflets are coupled by a free energy term that promotes orientational ordering in the hydrocarbon chains of one layer if the other layer orders. The model is analyzed to obtain phase diagrams for the bilayer. The dominant result is that phase separation in one leaflet drives phase separation in the other leaflet at the same temperature, although the difference between the separated phases in the second layer is weaker. In principle a further liquid-liquid phase separation is possible at lower temperature. The special case of coupled layers having the same composition is also studied. |
| Joachim Ankerhold | Freiburg | The Quantum Smoluchowski Equation Abstract: In this talk I will briefly discuss how the strong friction limit in quantum mechanics leads to the low temperature version of the classical Smoluchowski equation based on an exact description of dissipative quantum systems [1]. This in turn also shows that recent derivations by means of high temperature master equations are not consistent. As a specific application the phase diffusion of overdamped Josephson junctions is considered [2] and the changeover from coherent Cooper pair tunneling to Coulomb blockade discussed. Some recent extensions of this descriptions are addressed. References:
|
| Dean Astumian | Maine | The unreasonable effectiveness of equilibrium-like theory for
interpreting non-equilibrium experiments Abstract: There has been great interest in applying the results of statistical mechanics to single molecule experiements. Recent work has highlighted so-called non-equilibrium work-energy relations and Fluctuation Theorems that take on an equilibrium-like (time independent) form. Here I give a very simple heuristic example where an equilibrium result (the barometric law for colloidal particles) arises from theory describing the thermodynamically non- equilibrium phenomenon of a single colloidal particle falling through solution due to gravity. This simple description arises from the fact that the particle, even while falling, is in mechanical equilibrium (gravitational force equal the viscous drag force) at every instant. The results are generalized using Onsager's least dissipation approach for stochastic processes to derive time independent equations that hold for thermodynamically non-equilibrium (and even non-stationary) systems. These equations offer great possibilities for rapid determination of thermodynamic parameters from single molecule experiments. |
| Clemens Bechinger | Stuttgart | Surmounting barriers:
The benefit of hydrodynamic interactions Abstract: We experimentally and theoretically investigate the collective behavior of three colloidal particles that are driven by a constant force along a toroidal trap. Due to hydrodynamic interactions, a characteristic limit cycle is observed. When we additionally apply a periodic sawtooth potential, we find a novel caterpillar-like motional sequence that is dominated by hydrodynamic interactions and promotes the surmounting of potential barriers by the particles. |
| Sergey M. Bezrukov | Bethseda | Static and dynamic disorder in protein
folding: Fluctuating ion channels Abstract: By analyzing fluctuations in biochemical processes, it is possible to reveal their important kinetic features that are usually hidden in average rates. This is particularly true for a variety of modern techniques that can probe the functioning of proteins on a single-molecule level. Among the new questions to address is that of static and dynamic disorder in protein folding. While static disorder is seen as time-persistent deviations of individual reaction rates from their ensemble average, dynamic disorder can often be observed as rate variations with time. I discuss these phenomena using recent single-molecule enzymology experiments with a special emphasis on the channel-forming membrane proteins. |
| Chris Van Den Broeck | Diepenbeek | From Brownian motor to Brownian
refrigerator Abstract: Onsager symmetry implies that a Brownian motor, driven by a temperature gradient, will also perform a refrigerator function upon loading. We analytically calculate the corresponding heat flux for an exactly solvable microscopic model and compare it with molecular dynamics simulations. We show that, by a combination of the motor and refrigeration function, it is in principle possible to achieve Carnot effiency. References:
|
| Adi Bulsara | San Diego | Novel Coupling of Nonlinear Elements for Fun and Profit |
| Alexander Dubkov | Nizhni Novgorod | Langevin approach to anomalous diffusion in fixed potentials: Recent
results and perspectives Abstract: The direct derivation of closed fractional diffusion equation for probability density from Langevin equation with white Levy noise, based on the theory of infinitely divisible distributions, is proposed [1]. Describing the Markovian anomalous diffusion in the form of Levy flights, this equation gives a good opportunity to investigate a probabilistic and time characteristics of anomalous diffusion in different smooth potential profiles. We review recently obtained results regarding the stationary probability distributions, the rate of barrier crossing, and the features of resonant activation phenomenon for Levy flights. We derive also the exact equation to compute the mean lifetime (nonlinear relaxation time) for arbitrary smooth potential and solve it for the metastable cubic potential. The exact expression for the mean lifetime obtained by integration of the solution mentioned is used to analyze the peculiarities of noise enhanced stability (NES) phenomenon [2] in the case of anomalous diffusion. In conclusion, some perspectives of further investigations in this area are discussed. References:
|
| Werner Ebeling | Berlin | Several generalizations of
the Smoluchowski equation Abstract: We will give first an historical overview of several generalizations including internal coordinates and distances which were first given by Debye, Huckel, Onsager and Falkenhagen. Further we will discuss applications to electrolytes, polymers etc., and also give some overview on the statistical derivations by means of projection operators etc.. In the last part we will give new Smoluchowski-type equations for active Brownian particles. |
| Ralf Eichhorn | Bielefeld | Noise-induced enantiomer separation in a microfluidic channel Abstract: Two different molecules that are mirror images of each other, the so-called enantiomers, can possess very different functional properties in biological systems or as pharmaceuticals. For this reason, separation and analysis of enantiomers is of great importance. Recently, Kostur et al. [1] proposed a new separation scheme for enantiomers based on spatially variable vorticity of the flow in a microfluidic device. We investigate the motion of enantiomers in fluid flows through microchannels without vortices. We show that two different enantiomers can have different migration velocities along the channel, resulting in their separation. In discussing the underlying physical mechanism we identify the presence of thermal noise as an indispensable prerequisite. References:
|
| Fereydoon Family | Atlanta | Smoluchowski Rate Equation Approach to Cluster Size
Distribution: Beyond Mean-Field Abstract: Cluster nucleation and growth by aggregation is the central feature of many physical processes, from polymerization and gelation in polymer science, flocculation and coagulation in aerosol and colloidal chemistry, percolation and coarsening in phase transitions and critical phenomena, agglutination and cell adhesion in biology, to island nucleation and thin-film growth in materials science. Detailed information about the kinetics of aggregation is provided by the time-dependent cluster-size distribution, a quantity which can be measured experimentally. Based on the von Smoluchowski rate equations, considerable theoretical effort has been made toward a better understanding of the mechanisms determining the scaling properties of aggregation phenomena. While the standard rate-equation approach has been successful in predicting the scaling behavior of average quantities such as the total cluster density, when there are significant spatial fluctuations it gives predictions which are in significant disagreement with both experiments and kinetic Monte Carlo simulations. This failure can be traced to the fact that the usual mean-field approach does not include correlations between the size of an island and its local environment. Such correlations are especially important in lower dimensions, such as in cluster growth on surfaces. In this talk I will present a new method for calculating the cluster-size distribution which solves the long lasting problem of determining the correlations between the size of an island and that of its capture zone. Applying this method to submonolayer epitaxial growth, we show that by coupling a set of evolution equations for the capturezone distributions with a set of rate equations for the island densities one may obtain accurate predictions for the time and size-dependent rates of monomer capture. In particular, we show that by using this method one can obtain excellent results for the capture numbers and island-size dis tributions in irreversible growth on both one- and two dimensional substrates. |
| Henrik K. Flyvbjerg | Roskilde | Cell motility as persistent random motion:
theories from experiments Abstract: Cell migration is essential in many physiological and pathological processes and in emerging medical technologies that depend on it for colonization of biomaterials. Quantitative migration studies rely on motility models for data interpretation. Finding no model in the literature that captures the nature of our data, we used the data to capture the nature of suitable models. An analysis of trajectories followed by motile human keratinocytes and fibroblasts lead to cell-type-specific motility models. These models show that cells have memory, and apparently reflect the cells' different roles in the organism. The method of analysis is general and may be applied to other motile cell-types and organisms. |
| Andrzej Fuliński | Kraków | Asymmetries and anomalous phenomena in ionic transport through nanochannels Abstract: Biological and synthetic nanochannels exhibit two essential biophysical properties: selective ion conduction and the ability to gate open in response to appropriate stimulus. Both these properties are related to several untypical modes of behavior of the diffusional and conduction currents, absent in the normal (electro-)diffusion. We present our recent results concerning some of such anomalous phenomena. |
| Henryk Galina | Rzeszów | Smoluchowski coagulation equation in
modeling polymerization processes Abstract: The Smoluchowski coagulation equation was derived back in 1916. It is usually linked with diffusivity and size of aggregating particles. In its contemporary form it reads: (1) where ci is the number (concentration) of clusters of size i (i = 1, 2, ...) and the coagulation kernel Ki,j contains all the physics of the aggregation process. In 1944 Stockmayer used eq. 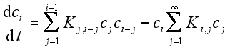 (1)
(1)to derive the size distribution of (macro)molecules formed in a polymerization process. Ki,j was then the rate coefficient at which molecules of size i reacted with those of size j. At present, the idea behind the Smoluchowski coagulation equation has been applied for various types of polymerization process. Its application revealed the significance of the so-called time correlations in the polymerization processes and their effect on the size distribution of polymer molecules. The method of using eq. (1) in polymer science will be outlined and its application in particular processes, e.g. for reducing molecular dispersity in hyperbranched polymerization. |
| Peter Hänggi | Augsburg | Quantum Brownian motion and Quantum Brownian motors |
| Robert Hołyst | Warszawa | Evaporation/condensation in a microscale Abstract: The evaporation/condensation processes are studied in the framework of diffuse interface hydrodynamics supplemented by the van der Waals equation of state. The processes are studied in the time scale from picoseconds to microseconds and in the length scale from tenth of nanometers to micrometers. The evaporation process proceeds quasistationary, governed by the heat flow along the temperature gradients. Condensation is never quasistationary. It proceeds two orders of magnitude faster than evaporation. Simple formula for evaporation rate of a liquid droplet is derived and compared with full solution of hydrodynamic equations. It shows that mass transfer during evaporation follows the heat flow. Finally it will be shown that vapor bubbles can be used, during condensation, as a high-temperature (2000 K for argon) fast (50 ps) microreactors at low temperature (280 K) of a surrounding fluid. This fact will bring the subject close to the sonoluminescence and sonochemistry. |
| Joseph Klafter | Tel Aviv | Searching a circular DNA strand: a stochastic approach Abstract: We introduce and explore a stochastic model of an enzyme searching for a target site on a circular DNA strand. The enzyme performs a local scan of the strand and occasionally, according to a given exponential rate, randomly relocates its position on the strand. The local scanning corresponds to a one-dimensional continuous motion on the strand, whereas the relocation corresponds to a 3D motion in the medium containing the strand. An analysis of the model proposed for general scanning and relocation mechanisms is carried out, and closed-form analytic formulae for the mean and Laplace transform of the overall search duration are computed. Thereafter, an asymptotic analysis for long DNA strands is conducted, yielding the limiting probability distribution of the overall search duration. The asymptotic analysis is further generalized to encompass the cases of parallel and massively-parallel searches performed by an ensemble of independent enzymes. The general results obtained are applied to the following examples of local scanning mechanisms:(i) directed linear motion, (ii)Brownian motion, (iii)fractional Brownian motion, and (iv) fractional Lévy motion. For these examples the asymptotically optimal relocation rates are calculated. |
| Howard Lee | Athens | Ergodic hypothesis in Hermitian many-body problems Abstract: The ergodic hypothesis (EH) says that the time and ensemble averages of a dynamical quantity are the same. The studies of its validity by ergodic theory or quasi-ergodic theory are far removed from physics. A more physically based study is to do the time averages and to compare it the ensemble average. This would be the most direct and clearest way of testing EH. Why has it not been done earlier? To do time averaging, one must know the time evolution of a dynamical variable by solving the Heisenberg equation of motion, itself no simple task. But now there are general solutions by the recurrence relations method. Thus the time averaging can be achieved. As a result, a new ergodic condition has been formulated and the physical mechanisms that underly EH have been found. |
| Katja Lindenberg | San Diego | Subdiffusion-Reaction Problems Abstract: Reactions between diffusive species in constrained geometries have long been known to exhibit kinetics that differ profoundly from mean field behavior, reflecting the importance of spatial and temporal fluctuations in these systems. When the reactive species are subdiffusive, the kinetics are yet again entirely different. We further explore these kinetics when the subdiffusive reactants are subject to competing decay processes, e.g., when the reactants have an intrinsically finite lifetime. |
| George Maret | Konstanz | Breakdown of photon transport due to Anderson localization Abstract: Constructive interference between reciprocal multiple scattering paths of waves in disordered media gives rise to coherent backscattering and Anderson localization. We report on optical coherent backscattering and time resolved transmission experiments on very turbid powders of high index colloidal particles. These samples have photon transport mean free paths l* close to or smaller than the wavelength 2pi/k and very weak absorption so that multiple scattering paths lengths up to 10m (> 10^7 scattering events) can be analyzed. We find a slowing down of the photon diffusion constant at long times which scales with kl* [1,2] in quantitative agreement with predictions of scaling theory of localization [3,4]. [1] M.Störzer, P.Gross, C.M.Aegerter, G.Maret, Phys.Rev.Lett. 96, 063904 (2006) [2] C.M.Aegerter, M.Störzer, G.Maret, submitted (2006) [3] E.Abrahams, P.W.Anderson, D.C.Licciardello, T.V.Ramakrishnan, Phys.Rev.Lett. 42, 673 (1979) [4] R.Berkovitz, M.Kaveh, J.Phys.Cond.Mat. 2, 307 (1990) |
| Maciej A. Nowak | Kraków | Brownian Walks of Large Matrices Abstract: We briefly discuss the method of free random variables, its relation to probability theory and to random matrices and we point at possible applicatons in a context of the stochastic diffusion theory. In order to demonstrate this approach, we apply the formalizm of free random variables for the cases of additive matrix diffusion and for matrix analogues of multiplicative Brownian walks. |
| Gábor Papp | Budapest | Two level system perturbed by
noise: the Random Matrix Theory Approach Abstract: By using the random matrix approach we solve analytically the model of an effective two-level system coupled to a noise reservoir represented by a random Wishart-Cauchy matrix. We compare the calculated spectral properties of the system with the numerically simulated results and outline possible applications of the model in the field of condensed phase reactions. |
| Jarosław Piasecki | Warszawa | Centenary of Marian Smoluchowski's kinetic theory of
the Brownian motion Abstract: Seminal ideas developed by Marian Smoluchowski in his 1906 papers on the diffusion and on the Brownian motion present the most creative application of the probability theory to the description of physical phenomena. |
| Eli Pollak | Weizmann Institute of Science | Hamiltonian theory of stochastic acceleration Abstract: Stochastic acceleration, defined in terms of a stochastic equation of motion for the acceleration, is derived from a Hamiltonian model. A free particle is coupled bilinearly to a harmonic bath through the particle's momentum and coordinate. Under appropriate conditions, momentum coupling induces velocity diffusion which is not destroyed by the spatial coupling. Spatial-momentum coupling may induce spatial subdiffusion. The thermodynamic equilibrium theory presented in this Letter does not violate the second law of thermodynamics, although the average velocity squared of the particle may increase in time without bound. |
| Harald A. Posch | Vienna | From diffusion to the colour of the sky: Marian Smoluchowski's scientific roots and his impact on statistical physics Abstract: Already during his studies in Vienna, Marian Smoluchowski was strongly affected by the fierce debate, which raged about the existence of atoms, and which, at the end of the 19th century, was preparing the grounds for a new science, theoretical physics. Ultimately, the probabilistic approach he pioneered already in his early work was decisive for the acceptance of the atomistic point of view. It also had a profound influence on the evolution of statistical physics as a whole. We demonstrate the implications of his work with a few examples. |
Jose Miguel Rubi | Barcelona | Fick-Jakobs kinetics for entropic transport
in quasi-onedimensional structures Abstract: We study nonlinear transport processes through quasi-onedimensional structures, as pores, ion channels and zeolites, exhibiting changes in their shape along the propagation direction. The constrained dynamics of the particles is analyzed by means of the Fick-Jakob equation for the probability distribution which assumes that particles evolves through entropic barriers. Our analysis reveals that entropic transport is distinctly different from that occurring though energy barriers. Applications to different dynamic situations are presented. |
| Francesc Sagues | Barcelona | Noise-mediated rhythms in active media
Abstract: I consider two scenarios of noise-mediated oscillatory regimes in extended active media. The first situation corresponds to the well-known BZ reaction in its photosensitive version. By forcing it with a spatiotemporally distributed noise we obtain a sustained target-like pattern of wave propagation from an otherwise (in absence of noise) purely excitable condition. Experimental, theroretical and numerical results will be briefly summarized (1). In the second scenario we propose a moel to explain the phenomenon known as plankton blooms. It is based on the coupling of an activator-inhibitor dynamics for two plankton populations with a turbulent flow field simulated in terms of a stochastic velocity field (2). References:
|
| Harvey Scher | Rehovot | Anomalous transport in geological formations: Theory and observations Abstract: Anomalous transport of chemical tracers has been observed at field and laboratory scales, in a wide variety of porous and fractured geological formations. Quantification of this widespread phenomenon has been a long-standing problem. These formations are heterogeneous on a very wide range of spatial scales and the difficulty in capturing the complexities of tracer plume migration patterns suggests that local heterogeneities cannot be "averaged out" even on small scales (as has been the practice). Recently, a theory developed within the continuous time random walk (CTRW) framework, based on a picture of transport as a sequence of particle transfer rates, has been demonstrated, via laboratory- and field-scale observations, to provide an effective means to quantify this anomalous transport. In highly disordered systems we show that statistically rare, slow transition rates limit transport. Hence, the key step is to retain the entire range of these transitions with a pdf (r,t), where r is a transition step displacement and t is the transfer time, instead of upscaling from mean local rates. The present application is shown to be a uniquely rich example of anomalous transport as the tracer plume and breakthrough curves can be measured directly. It has generated a new level of confirmation and further development of the theory. Most importantly, we have now developed the CTRW within the framework of partial differential equations (pde) and generalize its applicability to non-stationary domains (e.g., extended field sites) and interactions with "immobile states" (matrix effects). These pde's are non-local in time as they incorporate a memory function M(t), based on r (r,t), and the Laplace space form of them can be solved by both analytical and conventional numerical methods. We show that physical models of M(t) encompass full tracer (plume) dynamics with multirate mass transport, fractional-derivative- and advective-dispersion- equations as specialized cases. |
| Lutz Schimansky-Geier | Berlin | Low randomness in
ratchets and steppers Abstract: We introduce the diffusion coefficient and the Peclet-number as a measure of quality for transport in ratchets and for the motion of steppers. We calculate both for simple discrete ratchet models and give conditions which reduce randomness of the transport. In addition periodic forcing can be used to synchronize the motion of Brownian steppers which corresponds to a state with low randomness. J. A. Freund, and L. Schimansky-Geier, Phys. Rev. E 60, 1304 -1309 (1999). B. Lindner, M. Kostur, and L. Schimansky-Geier, Fluctuations and Noise Letters 1, R25 (2001). B. Lindner and L. Schimansky-Geier, Phys.Rev.Lett. 89, 230602 (2002). T Prager, L Schimansky-Geier and I M Sokolov, J. of Physics: Cond. Matter 17, 3661 (2005) |
| Michael F. Shlesinger | Arlington | Stretched Times and Divergent
Time Scales Near the Glass Transition |
| Igor M. Sokolov | Berlin | Response, fluctuations and reactions in
subdiffusive systems Abstract: Many physical systems showing subdiffusive behavior can be described within a framework of continuous time random walks (CTRW) with waiting time distributions lacking the mean. The corresponding random processes are not homogeneous in time. For example, the behavior of the system depends on the time elapsed from the instant when the system was prepared, the effect typically quoted as aging. More complicated aging effects arise in systems under influence of time-dependent fields and in reacting systems, where products of reaction are introduced into the system later in course of reaction. We discuss here the general problem of kinetic equation description of CTRW and related systems and illustrate the situation by several results pertinent to response of such systems to external fields, field-induced fluctuation effects and to behavior of reactions in systems under CTRW. |
| Bernardo Spagnolo | Palermo | Lifetime of metastable states and suppression
of noise in interdisciplinary physical models Abstract: Metastability is a generic feature of many nonlinear systems, and the problem of the lifetime of metastable states involves fundamental aspects of nonequilibrium statistical mechanics. The investigation of noise-induced phenomena in far from equilibrium systems is one of the approach used to understand the behaviour of physical and biological complex systems. The enhancement of the lifetime of metastable states due to the noise and the suppression of noise through resonant activation phenomenon will be discussed in models of interdisciplinary physics: (i) dynamics of an overdamped Josephson junction; (ii) transient regime of the noisy FitzHugh-Nagumo model; (iii) population dynamics. |
| Peter Talkner | Augsburg | Long-time behavior of driven Smoluchowski processes with metastable states |
| Horacio S. Wio | Santander | Stochastic resonance in extended systems: general
nonequilibrium potential framework Abstract: Many phenomena related to Stochastic resonance (SR) occur in extended systems, a fact that together with the possible technological applications, motivated many recent studies showing the possibility of achieving an enhancement of the system's response by means of the coupling of several units in what conforms an extended medium. In a series of papers [1] we have studied the SR phenomenon in extended systems, when transitions between two different spatial patterns occurs (i.e. bistability). This was done exploiting the concept of non-equilibrium potential (NEP) [2]: a Lyapunov functional of the associated deterministic system that, for non-equilibrium systems, plays a role similar to that of a thermodynamic potential in equilibrium. Such NEP characterize the global properties of the dynamics: attractors, relative stability of these attractors, height of the barriers separating attraction basins. In addition, it allows us to evaluate the transition rates among the different attractors. Here I will report on how some known forms of the NEP, for scalar as well as many component systems, could be exploited in order to analyze SR in extended systems. I will discuss, from the NEP's viewpoint, several aspects: the effect of the NEP's symmetry, of density-dependent coupling, the role played by local and non-local couplings, as well as the possibility of other related phenomena like the so called "system-size SR". I will also show a way to evaluate the amplification factor as a measure of the SR response in extended systems. [1] H.S.Wio, Phys.Rev. E 54, 3045 (1996); F.Castelpoggi, H.S.Wio, Europhys.Lett. 38, 91 (1997) and Phys.Rev. E 57, 5112 (1998); S.Bouzat, H.S.Wio, Phys. Rev. E 59, 5142 (1999); B.von Haeften, R.Deza, H.S.Wio, Phys.Rev.Lett. 84, 404 (2000); H.S.Wio, S.Bouzat, B.von Haeften, [Proc. STATPHYS21: 21st IUPAP International Conf. on Statistical Physics], Physica A 306C, 140 (2002); B.von Haeften, et al, Phys. Rev. E 69, 021107 (2004); B.von Haeften, G.G. Izus and H.S.Wio, Phys. Rev. E 72 (2), 021101 (2005). [2] R.Graham, in "Instabilities and Nonequilibrium Structures", Eds.E.Tirapegui and D.Villaroel (D.Reidel, Dordrecht, 1987); H.S. Wio, in "4th. Granada Seminar in Computational Physics", Eds. P. Garrido and J. Marro (Springer-Verlag, Berlin, 1997), pg.135. |
| Wojbor A. Woyczynski | Cleveland | Large scale structure of the universe and scaling
limits for clasical and anomalous conservation laws Abstract: Burgers turbulence is one of the accepted formalisms for the adhesion model of the large-scale distribution of matter in the Universe. Variational methods can be used to establish evolution, in the scaling limit, of the quasi-Voronoi tesselation structure of shock fronts dependent on random potentials and initial data. Self-similar solutions can also play an important role in studies of anomalous conservation laws. |
| Jakub Zakrzewski | Kraków | Atomic physics meets condensed matter physics |
| Claudio Zannoni | Bologna | The intertwining of structure and dynamics in liquid crystals Abstract: Molecular organization (structure) and dynamics are strictly coupled in liquid crystals (LC), as shown, for instance, by the classical Nordio-Smoluchowski stochastic equation for the molecular reorientation of a molecule in uniaxial nematics [1,2], where the phase structure enters with an effective anisotropic molecular field. This equation has been generalized in many ways, e.g. to more complex biaxial and, recently, chiral solutes and phases [3]. However, while these equations are invaluable in analyzing experimental data for a variety of techniques, the number of structural and dynamical parameters they require rapidly increases, making their predictive power relatively limited. On the other hand computer simulations of liquid crystals have made important progresses and molecular [4] and atomistic [5] resolution models have become increasingly important. In particular reasonable predictions of the nematic-isotropic transition temperatures from atomistic molecular dynamics now start to become feasible for realistic systems [6]. Here we shall discuss how state of the art computer simulations can now be used to provide some important information that complements stochastic models, and how the two approaches can to some extent be combined. In particular we shall show some recent examples for the structure and dynamics of the popular nematic 4-pentyl, 4'-cyano biphenyl 5CB [7]. References:
|
| If you are not an invited speaker, you may present a poster. | ||
| Posters | ||
| Michael Alania*, Renata Modzelewska, Anna Wawrzyńczak-Szaban | Tbilisi*, Siedlce | Einstein – Smoluchowski equation and problem of
galactic cosmic ray time-dependent modulation
Abstract: We developed a time-dependent model based on the Parker's transport equation to describe a propagation of galactic cosmic rays (GCR) in the interplanetary space. The model is five dimensional - time t and rigidity R dependent partial differential equation in the spherical coordinate system (r, q, j). We numerically solve this 5-D partial differential equation assuming that the scattering of GCR particles in the irregularities (turbulence) of the interplanetary magnetic field (IMF) can be considered as a Brownian motion and the Einstein-Smoluchowski relation is valid. |
| Przemysław Borys | Gliwice | On the mathematics of Ball and Chain models Abstract: |
| Olgierd Cybulski | Warszawa | Spontaneous oscillations of a two-phase flow in a
microfluidic network Abstract: We study pressure-driven flow of a liquid containing droplets of another fluid through a network of microchannels. The droplets flow into the network at constant frequency, at intervals T. When a droplet arrives at the point in which the channel branches into two, it enters the channel where the volumetric flow is larger. However, the presence of droplets in channel affects its hydrodynamic resistance, so that two subsequent droplets do not have to choose the same way. This system displays two paradigm features of non-linear systems: amplification of the sligthest difference between the inflow into the branches to a binary choice of the trajectory, and the feedback between subsequent choices through the long range interactions transmitted via the distribution of pressure in the system. We investigate the dynamics of this system for large occupancies of the network by the droplets. For many simple networks we observe that the system achieves a stationary state and the number of droplets in each channel stabilizes at a constant level (with fluctuations not greter than few droplets). Surprisingly, there are also networks for which the stationary state does not exist. Instead, we observe spontaneous oscillations of the number of droplets in the channels, with an amplitude much larger than one droplet and a period much longer than T. |
| Carmen Schmitt, Bartłomiej Dybiec, Peter Hänggi, Clemens Bechinger, | Stuttgart, Kraków, Augsburg | Experimental study of resonant activation Abstract: Resonant activation is a generic effect for the barrier crossing dynamics of temporally modulated energy landscape. Here the escape of a Brownian particle over a periodically modulated double-well potential barrier is investigated experimentally and numerically. The problem of resonant activation is revisited with the attention on the effect of periodic modulation of the barrier on optimal value of the mean escape time in the system. The experimental measurements of the resonant activation phenomenon in a colloidal system are accompanied with computer simulations. |
| Alessandro Fiasconaro | Palermo | Extinction statistics in N random interacting species Abstract: An N-species Lotka-Volterra system randomly interacting in the presence of a multiplicative noise is analyzed. The investigation is focused on the statistical properties of the extinction times of the populations. The role of the external noise on the extinction statistics is studied. |
| Agnieszka Gil-świderska, Renata Modzelewska, Michael V. Alania | Siedlce, Tbilisi | On the 27–day variation of the galactic cosmic
rays intensity and anisotropy Abstract: We propose a new model to describe the-27 day variations of the galactic cosmic ray (GCR) intensity and anisotropy based on the Parker’s transport equation. In the model are included the heliolongitudinal asymmetries of the solar wind velocity and the interplanetary magnetic field (IMF) turbulence among other classical processes responsible for the GCR modulation in the interplanetary space. We found that the distinction of the amplitudes of the GCR intensity and anisotropy in different the positive (A>0) and the negative (A<0) polarity epoch is caused by the heliolongitudinal asymmetry of the GCR particles convection due to drift in the regular heliospheric magnetic field. We estimated an influence of the character of the radial decay of the heliolongitudinal asymmetries of the solar wind velocity and the IMF turbulence on the expected amplitudes of the 27-day variations of the GCR intensity and anisotropy. The theoretical calculations are compared with the exper imental results obtained by neutron monitors data for different the A>0 and A<0 epoch of solar cycle. We believe that the proposed model is compatible to describe the-27 day variations of the GCR intensity and anisotropy in the energy range of 5-50GeV. |
| Helmuth Huffel | Vienna | Active Stochastic Quantization Abstract: Stochastic quantization provides an interesting connection between quantum field theory and statistical mechanics, with new applications especially in gauge field theories. Euclidean quantum field theory is viewed as the equilibrium limit of a statistical system coupled to a thermal reservoir; the Euclidean Green functions become identical to stochastic averages. Active stochastic quantization is a proposed generalization of this quantization scheme by employing active brownian motion. |
| Adam Kleczkowski, Piotr Kleczkowski | Cambridge, Kraków | Monte-Carlo Methods for Shaping Time-Frequency Areas for the
Selective Mixing of Sounds Abstract: The method of Selective Mixing of Sounds is an innovative technology in audio engineerging. It is a non-linear process in which we attempt to reduce the information from several tracks of audio during the otherwise routine operation of mixing these tracks to a single track in a musical recording. The most conceptually challenging element of the method is a procedure of determining areas of the time-frequency plane in which a single track is dominating. The procedure needs to take into account the information about the energy transmitted in each track at a given time-frequency combination. However, using local information only leads to high distortions of the signal and rapid switching among tracks. A smoothing technique is necessary to produce large and compact areas of dominance by a single instrument. The smoothing also needs to preserve shapes important for the perception of tone colour, sound attack and decay and other features, characteristic for different instruments. The choice of a particular method has a major effect on the overall quality of the sound. We propose a range of novel methods, based on an iterative Monte-Carlo approach. While computationally expensive, these methods are very flexible. The approach focuses here on a single time-frequency event and uses a set of deterministic or probabilistic rules to assign to it a particular track. The selection depends not only on the properties of all tracks at the event, but also on its neighborhood. The rules are then applied sequentially to all events, either in a systematic or random order. The procedure is then repeated until the required level of smoothing is achieved. In this way, the selection of a dominant track for any given time-frequency event is based on a large number of events. This allows preservation of some characteristic details of an instrument, while selecting the most important signal for each area of the time-frequency plane. |
| Robert Kosiński, Andrzej Grabowski | Warszawa | Properties of evolving directed network with local rules and intrinsic variables Abstract: We present a model of evolution of directed network, based on local rules. It generates a complex network with the properties of real systems, like scale-free distribution of outgoing and ingoing connectivity. Each node is characterised by intrinsic variable S, and number of outgoing links kout. As a result of network evolution, the number of nodes and links, as well as their location, change in time. For critical values of control parameters a transition to a scale-free network is observed. Our model reproduce also others nontrivial properties of real networks, e.g. large clustering coefficient and lack of correlations between age of a node and its connectivity. |
| Małgorzata Kotulska*, Krystian Kubica*, Stanisława Koronkiewicz, Sławomir Kalinowski | Wrocław*, Olsztyn | Monte Carlo model of the induction of lipid membrane
electropermeabilization. Abstract: The phenomenon of electroporation is preceded by induction and expansion of defects, responsible for the pre-pore excitation. We examine the mechanism of the induction of the field-driven defects by Monte-Carlo simulations. The study is based on the improved Pink model, which includes explicit interactions between polar heads and energy of interactions between the heads and the field. No anomalous deformation of the molecules is allowed. The study, provided for bilayer dipalmitoyl-phosphatidylcholine (DPPC) membrane in the gel (300 K) and fluid (330 K) phases, shows dependence of the membrane conformational and energetical state on the value of electric field. We observe that the electric field affects the number of molecules in the gel and in the fluid states. In the layer at the negative potential, when the transmembrane voltage is above Uc ~ 280 mV, lipid heads abruptly reorient and the number of local spots with fluid conformation increases. The other layer slightly tends to tighten its structure, producing additional mechanical stress between layers. Lipids showed complete insensivity to electric field within physilogical limits, U < 70 mV. |
| Tadeusz Kosztołowicz*, Katarzyna D. Lewandowska**, Michał Penkowski** | Kielce*, Gdańsk** | Application of hyperbolic subdiffusion equation to
study the electrochemical impedance Abstract: We use the hyperbolic subdiffusion equation with fractional time derivatives (generalized Cattaneo equation) to study the transport process of electrolytes in gels and porous medium. In particular, we apply the equation to obtain, for a process with non-vanishing relaxation time, the formula of electrochemical impedance in a spatially restricted sample. Comparing the theoretical formulas with the experimental Cole-Cole plots of impedance, we find the parameters describing the transport (such as subdiffusion parameters and relaxation times) for the investigated materials. |
| Małgorzta Krawczyk, Krzysztof Kułakowski | Kraków | Formation of DNA networks - computer simulations Abstract: Continuous search for potential applications of DNA is motivated by special features of the DNA molecules. In particular, it is possible to construct networks of DNA [1,2]. Here we report results of the computer simulation of a formation of networks from two kinds of molecules: linear and branched (Y-shaped). The simulation is performed on a basis of two-dimensional triangular lattice. Our aim is to analyze the distribution of the pore size in the network, as dependent on the concentration of DNA in the system. Here we demonstrate, that the obtained distribution does not depend on the density of the branched molecules. References:
|
| Natalia Kruszewska, Adam Gadomski | Bydgoszcz | How to get 2D model biopolymer polycrystals based on a
mesoscopic Smoluchowski-type dynamics supplemented by computer experiment?
Abstract: Based on a Smoluchowski-type model, formulated in a phase space of the linear object's size (relevant stochastic variable) in terms of the mesoscopic nonequilibrium thermodynamics (MNET) [1] as a guiding formalism, we are looking for its basic trends and characteristic features in a suitably designed computer experiment [2]. It turns out that the basic and most interesting trends are recovered, although both ways, i.e. MNET and computer model, are sometimes able to see things for their own in a profitable way. It implies that both approaches are useful in examining, e.g. biopolymer polycrystals termed cylindrolites [3]. References:
|
| Michał Kurzyński | Poznań | Effects of vibratonal nonequilibrium on fast
nonadiabatic processes of energy and charge transfer
Abstract: Considerable developments in ultrafast laser spectroscopy offer a powerful tool for studying the very initial stages of photosynthesis. These involve the energy transfer within an antenna system followed by the primary electron transfer in a reaction centre and last no longer than few picoseconds. Of a similar rate are processes of vibrational relaxation which, consequently, have to be taken into account in the correct description of the phenomenon. In a few recent papers, this was done by numerical solving of a complex system of quantum master equations. Here, a simplified formalism is proposed combining transition processes with diffusion in an energy space. Analytical formulae for effective rate constants for the transitions are derived and a transient kinetics is considered. The model explains a peculiar temperature and wavelength dependence of pomp-probe spectra observed. |
| Marek Litniewski | Warszawa | Molecular dynamics study on the influence of the quencher concentration on the rate of simple
bimolecular reaction
Abstract: The influence of quencher concentration on the rate of the reaction: A+B –> C+B (B – quencher) is analyzed by performing large scale computer simulations [1,2]. The reagents are represented by identical soft spheres. Two different types of systems are considered: simple liquids at high and moderate density described by deterministic MD and very low density systems in which the spheres are immersed in the Brownian medium. It is shown that the excess in the rate coefficient caused by the finite quencher concentration is not universal and manifests specific behavior depending on considered system. For the deterministic systems the excess is positive for short times and negative in the long time limit. For the Brownian systems the excess is always positive and, except for very short times, constant. It is also shown that the relative excess in the surviving probability for a very wide range of time can be described by an universal quadratic function of the quencher co ncentration. A very strong correlation between the excess in relative value of spatial correlations between the reagents and the excess in the rate coefficient is observed. It is also shown that the A-A and A-C interactions have some influence on the excess values. A simple model for this effect is presented. References:
|
| Krzysztof Małysiak, Zbigniew Grzywna | Gliwice | On the Ball and Chain Model by Simple Diffusion Abstract: |
| Alexey Nikulov | Chernogolovka | Smoluchowski's consideration of limits of the second law of thermodynamics is topical again Abstract: Thoughts of great scientists, on the one hand, seem obvious and, on the other hand, keep topicality during a long time. The point of view by Marian Smoluchowski on the second law of thermodynamics expounded in [1] seems obvious for physicists of 20 century although it is written in this paper that most scientists of 19 century rejected the atomic-kinetic theory of heat. Smoluchowski was first who argued why the perpetuum mobile is not possible in spite of the persistent equilibrium motion, for example, of Brownian particles. This argumentation repeated by Richard Feynman in his well known consideration of the ratchet/pawl combination [2] seems indubitable. Nevertheless the problem of limits of the second law is topical now as well as the century ago [3,4]. The argumentation by Smoluchowski is based on a firm foundation: any equilibrium motion can not be ordered because of chaotic equilibrium motion of all. This equality of universal motion prevent a breach of symmetry because of an direct equilibrium motion. The postulate on impossibility of any direct equilibrium motion seems self-evident because of the equality of directions in space. Nobody could make doubt of the equal probability of motion in opposite directions since if anybody says that a right direction has higher probability than opposite one he should explain why no left. But even this self-evident postulate is violated in quantum systems [5]. It will be explained in the present work on the example of the experimental result considered in [6] why the Bohr’s quantization violates symmetry of equilibrium motion and challenges the second law. References:
|
| Anna Ochab-Marcinek, Ewa Gudowska-Nowak, Alessandro Fiasconaro, Bernardo Spagnolo | Krakow, Palermo | Co-occurrence of resonant
activation and noise-enhanced stability in the Michaelis-Menten
model Abstract: We investigate a stochastic version of a simple enzymatic reaction which follows the generic Michaelis-Menten kinetics. At sufficiently high concentrations of reacting species, the molecular fluctuations can be approximated as a realization of a Brownian dynamics for which the model reaction kinetics takes on the form of a stochastic differential equation. After eliminating a fast kinetics, the model can be rephrased into a form of a one-dimensional overdamped Langevin equation. We discuss physical aspects of environmental noises acting in such a reduced system, pointing out the possibility of coexistence of dynamical regimes where noise-enhanced stability and resonant activation phenomena can be observed together. |
| Rafał Orlik, Antoni C. Mitus, A.Z. Patashinski, M. Ratner | Wrocław | Local structure percolation in 2D Lennard-Jones liquid Abstract: The concept of precolation on lattices is generalized onto the case of locally ordered but globally disordered systems. These ideas are applied to a 2D Lennard-Jones liquid simulated using molecular dynamics method. We find that local solid-like structures precolate close to the liquidus line. |
| Otto Riefert, Antoni C. Mitu´s, | Wolfsburg, Wrocław | On local solid-like order in 2D Lennard-Jones liquid Abstract: The concentration of local solid-like structure in 2D Lennard-Jones liquid is analyzed using earlier proposed probabilistic analysis. The line (narrow domain) where this concentration becomes negligible is found, and constitutes a natural continuation in the pressure-temperature thermodynamic plane of the gas-liquid coexistence line. The question of related anomalies of physical parameters is briefly discussed. |
| Piotr Romiszowski, Andrzej Sikorski, Piotr Adamczyk | Warszawa | Structure of polymer chains in an adsorbing slit. a
Computer simulation study
Abstract: The aim of the study was the investigation of polymer molecules located between two parallel and impenetrable attractive surfaces. The chains were constructed of united atoms (segments) and were restricted to knots of a simple cubic lattice. Each polymer consisted of three chains of equal length emanating from a common origin (a uniform star). Since the chains were at good solvent conditions the only interaction between the segments of the chain was the excluded volume effect. The properties of the model chains were determined by means of Monte Carlo simulations with a sampling algorithm based on chain's local changes of conformation. The influence of the chain length, the size of the slit and the strength of adsorption on the structure of the system were studied. The differences and similarities in the structure (tails, trains, loops and bridges) for different adsorption regimes and size of the slit were shown and discussed. The dynamic behavior of the chain's structural elements was also studied. |
| Krzysztof Sadlej | Warszawa | Statistical description of a non-Brownian suspension Abstract: |
| Julian Sienkiewicz, Piotr Fronczak, Janusz A. Hołyst | Warszawa | Discrete effects on average path length scaling in
complex networks Abstract: We show that, depending on the network's average degree, mean distance in scale-free and random complex networks may exhibit deviations from well known scaling laws such as dependence on logarithm of network's size or logarithm of degrees product. It can be shown both analiticly and using numerical simulations that this behavior has its origin in discretization of path length distributions. A discussion about relevance of this feature to applications of real-world complex networks is presented. |
| Andrzej Sikorski, Dominik Gront | Warszawa | Thermodynamic properties of polypeptide chains.
Parallel tempering monte carlo simulations
Abstract: A coarse-grained model of polypeptide chains was designed and studied. The chains consisted of united atoms that represented amino acid residues. The united atoms were located at the positions of alpha carbons and were restricted to a [310] type lattice. Two kinds of united atoms were defined: hydrophilic and hydrophobic ones. The sequence of united atoms in the chain was assumed to be characteristic for a-helical proteins (the helical septet). The force field used consisted of the long-range contact potential between a pair of residues and the local potential preferring conformational states, which were characteristic for a-helices. In order to study the thermodynamics of our model we employed the Parallel Tempering (the Replica Exchange) Monte Carlo sampling scheme combined with the Multihistogram method. The optimal set of temperatures for the Parallel Tempering simulations was found by an iterative procedure. Starting from energy observations at different temperatures we computed the density of states for the system. Then, it was possible to recalculate any parameter of interest (such as the radius of gyration or energy components) as a continuous function of the temperature via averaging over the canonical ensemble. The influences of the temperature and the force field on the properties of coil-to-globule transition were also studied. |
| Marek Siłuszyk, K. Iskra, M. V. Alania* | Siedlce, Tbilisi* | Long-period modulation of the galactic cosmic rays
intensity and the interplanetary magnetic field turbulence
Abstract: To study the relationship between the temporal changes of the interplanetary magnetic field (IMF) turbulence and the rigidity spectrum of the galactic cosmic ray (GCR) intensity variations data of neutron monitors and of the IMF were used. The calculations were performed for the four ascending and four descending phases of solar activity (1960-2002) including the positive (A>0) and the negative (A<0) polarity periods of solar magnetic cycle. The soft rigidity spectrum of the GCR intensity variations for the maximum epoch and the hard one for the minimum epoch obtained by the worldwide network of neutron monitors data we ascribe to the essential rearrangement of the structure of the interplanetary magnetic field (IMF) turbulence in the range of the frequencies (10-6 – 10-5)Hz throughout the 11-year cycle of solar activity. There is not found any difference between the changes of the rigidity spectrum of the 11-year variations of the GCR intensity for different the A>0 and the A<0 polarity epoch. Taking account a strong relationship between the energy range of the IMF turbulence and the rigidity spectrum of the GCR intensity variations we conclude that the structure of the IMF turbulence significantly changes versus solar activity, while it does not change versus the A>0 and the A<0 polarity epoch of solar magnetic cycle. We propose the rigidity spectrum exponent of the GCR intensity variations as a new index to study the 11-year variations of GCR intensity and to estimate the state of the energy range of the IMF turbulence. |
| Łukasz Skowronek, P. F. Góra | Kraków | Chaos in Newtonian iterations: Searching for zeros which are not there Abstract: We show analytically that Newtonian iterations have a positive topological entropy. In a specific example of "solving" the equation x2+1=0, we analytically find the invariant density and show how this problem relates to that of a piecewise linear map. |
| Jędrzej Szymański | Warszawa | Nanorheology of surfactant micellar solutions from
protein diffusion Abstract: The Fluorescence Correlation Spectroscopy was used to determine the diffusion coefficients of proteins and dye molecules in the buffered solutions of C12E6 nonionic surfactant. The viscosity of the solution was extracted from the Einstein-Stokes relation. We showed that dynamics of proteins in the solution is heterogenous and consequently viscosity felt by the protein depends on its size, L, equal to twice the hydrodynamic radius. In the case of small proteins (e.g. lysozyme, L=3.8 nm) the nanoviscosity is order of magnitude smaller than the macroviscosity. From the size dependence of viscosity found in our experiments we estimated that in the case of our system we reach the macroscopic viscosity for L~20 nm. This means that the system becomes homogenous (for diffusion) at the length scale larger than 20 nm. |
| Marcin Tabaka | Warszawa | Stochasticity in gene expression Abstract: Biochemical reactions that take place at the level of a single cell typically include small numbers of molecules (e.g. 10-400). The complex inner structure of the cell makes up for heterogenous distribution of these molecules. Spatial fluctuations of the concentration of the reagents may introduce noise into biochemical pathways. We apply GFRD method to simulate genetic pathway of tryptophan regulation in Escherichia coli. |
| Davide Valenti*, L. Schimansky-Geier**, X. Sailer**, and B. Spagnolo* | Palermo*, Berlin** | Moment Equations in a Lotka-Volterra extended system
with time correlated noise Abstract: A spatially extended Lotka-Volterra system of two competing species in the presence of two correlated noise sources is analysed: (i) an external multiplicative time correlated noise which mimics the interaction between the system and the environment; (ii) a dichotomous stochastic process, whose jump rate is a periodic function, which represents the interaction parameter between the species. The moment equations for the species densities are derived in Gaussian approximation using a mean field approach. Within this formalism we study the effect of the external time correlated noise on the ecosystem dynamics. Finally we compare these results with those obtained studying the system dynamics within a coupled map lattice model. |
| Aleksander Weron, Marcin Magdziarz | Wrocław | Fractional stable noise. From Statistical Physics to
Financial Engineering Abstract: The starting point is the unique BRW (1998) decomposition of every self-similar stable noise into three independent components: mixed fractional motion, harmonizable and evanescent processes. We will analize the asymptotic dependence structure of fractional Ornstein-Uhlenbeck type noise and detect long and short range dependence. Some applications to anomalous diffusion as well as to option pricing in the context of term structure (Vasicek model) will be presented in details. |
| Maciej Wołoszyn, Bartłomiej J. Spisak | Kraków | One-dimensional systems with correlated disorder in
phase space Abstract: We consider the localization properties of electrons in one-dimensional systems with correlated disorder. The phase space formalism based on the quasi-distribution functions is applied to the description of such systems. The Renyi-Wehrl entropy is calculated from the Husimi function and used for reconstructing the localization properties. |
| Aleksander Woziński, Jan Iwaniszewski | Toruń | Surmounting fluctuating barriers in the presence of Kangaroo multiplicative noise Abstract: |
| invited speakers |
||
| titles and abstracts |
||
| fees |
||
| deadlines |
||
| participants |
||
| proceedings |
||
| location & lodging |
||
| important ! |
||
| gallery |
||