
Department of Field Theory
|
Our research.
(click the topic to learn more)
|
Relativistic quantum mechanics. Classical limit of quantum mechanics.
Majorana particles. 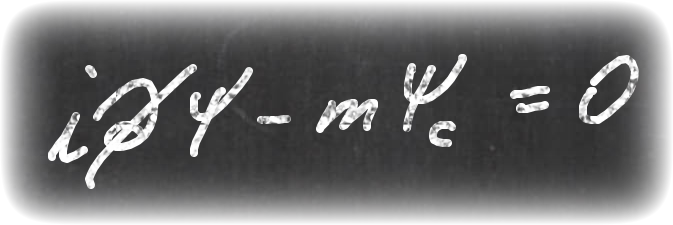 The most popular quantum models employ complex Hilbert spaces, however, the case of Majorana particle is an exception: here a real Hilbert space is relevant. This fact has rather interesting consequences, in particular, the standard momentum operator does not belong to the set of observables for the Majorana particle, and the procedure of quantization of the real fermionic Majorana field has to be worked out anew.
The problem of the classical limit of quantum theories includes the question of interactions of quantum systems with a macroscopic environment, where especially interesting is the theoretical description of the special physical processes known as measurements performed on quantum systems.
The most popular quantum models employ complex Hilbert spaces, however, the case of Majorana particle is an exception: here a real Hilbert space is relevant. This fact has rather interesting consequences, in particular, the standard momentum operator does not belong to the set of observables for the Majorana particle, and the procedure of quantization of the real fermionic Majorana field has to be worked out anew.
The problem of the classical limit of quantum theories includes the question of interactions of quantum systems with a macroscopic environment, where especially interesting is the theoretical description of the special physical processes known as measurements performed on quantum systems.
|
|
|
Conformal Field Theory. Matrix models. Topological reccurence,
Supersymmetry in noncommutative geometry. 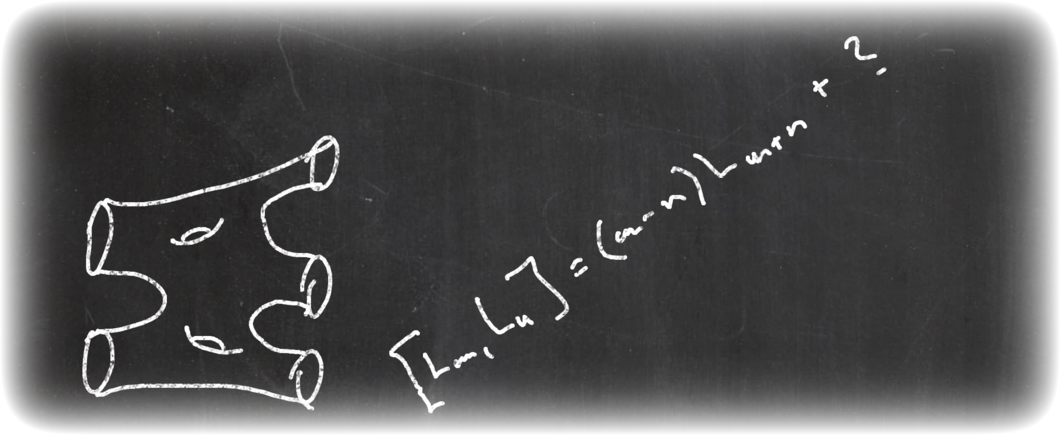 Symmetry is one of the most fundamental concepts of theoretical physics. It allows to understand universal properties of physical sytems, ̏organize” them into matematical structures and sometimes provides exact solutions of complicated models. Conformal field theory, matrix models (and topological recurrence which allows to solve them), super-symmetry, higher symmetries, infinite dimensional (symmetry) algebras or non-commutative geometry: all capture some aspects of symmetry and can be investigated both because of their physical relevance and mathematical beauty.
Symmetry is one of the most fundamental concepts of theoretical physics. It allows to understand universal properties of physical sytems, ̏organize” them into matematical structures and sometimes provides exact solutions of complicated models. Conformal field theory, matrix models (and topological recurrence which allows to solve them), super-symmetry, higher symmetries, infinite dimensional (symmetry) algebras or non-commutative geometry: all capture some aspects of symmetry and can be investigated both because of their physical relevance and mathematical beauty.
|
|
Quantum electrodynamics and its asymptotic structure.
Infrared problems in quantum field theory  Among fundamental problems of quantum electrodynamics, its infrared structure, asymptotic behavior and particle content ("infraparticle problem") belong to most interesting, and at the same time not fully understood. We investigate these problems with the use of known algebraic tools, and original ideas on judicious choice of gauge and on asymptotic algebra of fields.
Among fundamental problems of quantum electrodynamics, its infrared structure, asymptotic behavior and particle content ("infraparticle problem") belong to most interesting, and at the same time not fully understood. We investigate these problems with the use of known algebraic tools, and original ideas on judicious choice of gauge and on asymptotic algebra of fields. Inspired by quantum electrodynamics, but having wider applicability, is the question of backrection of a quantum system to changing external conditions ("Casimir effect"). We investigate this problem with the algebraic tools of quantum theory. |
|
|
Numerical methods in general relativity (accretion disks).
 Axially symmetric stationary Einstein equations describe self-gravitating disks around spinning and spinless
black holes and be integrated numerically, using a scheme based on a method developed by Shibata. The models
are used to describe tight black
hole-torus systems produced during coalescences of two neutron stars or
in modelling of compact active galactic nuclei.
Axially symmetric stationary Einstein equations describe self-gravitating disks around spinning and spinless
black holes and be integrated numerically, using a scheme based on a method developed by Shibata. The models
are used to describe tight black
hole-torus systems produced during coalescences of two neutron stars or
in modelling of compact active galactic nuclei.
|
|
|
Solitons, topological solitons, oscillons, skyrmions and their applications.
 Solitons are particle-like solutions of nonlinear field theories
preserving their shapes and sizes in most interactions. Their
applications span from subatomic level (as Skyrmions in effective models
for the low energy limit of QCD) through kinks in graphene, waves in
Bose-Einstein condensates, tsunami, neutron stars to cosmological
strings. They participate in quite interesting processes such as
annihilation with multiple fractal thresholds, negative radiation
pressure, staccato relaxation and bounces from force fields in
a form of spectral walls. Annihilation leads often to a formation of
oscillons which are extremely long-lived almost periodic states. By some
oscillons are considered as one of the candidates for dark matter.
Solitons are particle-like solutions of nonlinear field theories
preserving their shapes and sizes in most interactions. Their
applications span from subatomic level (as Skyrmions in effective models
for the low energy limit of QCD) through kinks in graphene, waves in
Bose-Einstein condensates, tsunami, neutron stars to cosmological
strings. They participate in quite interesting processes such as
annihilation with multiple fractal thresholds, negative radiation
pressure, staccato relaxation and bounces from force fields in
a form of spectral walls. Annihilation leads often to a formation of
oscillons which are extremely long-lived almost periodic states. By some
oscillons are considered as one of the candidates for dark matter.
|
|
|
Noncommutative Geometry. Hopf algebras and quantum groups.
Applications of Noncommutative Geometry in physics.  Noncommutative Geometry is, in a very broad sense, a generalization of geometry that allows to deal with spaces
that are no longer smooth manifolds or are 'quantum manifolds' described only by algebras. It offers an amazing
perspective for a theoretical physicists as a tool: to describe all physical objects as geometric objects, including
metric, gauge fields, Higgs field and fundamental fermions. With quantum spacetime being the most likely effect of quantum gravity, noncommutative geometry offers an insight into a mathematical structure of these objects, while quantum groups
and Hopf algebras provide a new extension of symmetries beyond the realm of groups. To see why the pricture represents
a noncommutative space and learn more about it - please visit this page
Noncommutative Geometry is, in a very broad sense, a generalization of geometry that allows to deal with spaces
that are no longer smooth manifolds or are 'quantum manifolds' described only by algebras. It offers an amazing
perspective for a theoretical physicists as a tool: to describe all physical objects as geometric objects, including
metric, gauge fields, Higgs field and fundamental fermions. With quantum spacetime being the most likely effect of quantum gravity, noncommutative geometry offers an insight into a mathematical structure of these objects, while quantum groups
and Hopf algebras provide a new extension of symmetries beyond the realm of groups. To see why the pricture represents
a noncommutative space and learn more about it - please visit this page
|